The unit of volume of a sphere is given as the 3. The metric units of volume are cubic meters or cubic centimeters while the USCS units of volume are, cubic inches or cubic feet. The volume of sphere depends on the radius of the sphere, hence changing it changes the volume of the sphere. There are two types of spheres, solid sphere, and hollow sphere. The volume of both types of spheres is different. We will learn in the following sections about their volumes.
For example, the space that a substance or 3D shape occupies or contains. Volume is often quantified numerically using the SI derived unit, the cubic metre. Volumes of some simple shapes, such as regular, straight-edged, and circular shapes can be easily calculated using arithmetic formulas.
Volumes of complicated shapes can be calculated with integral calculus if a formula exists for the shape's boundary. One-dimensional figures and two-dimensional shapes are assigned zero volume in the three-dimensional space. Using the volume formulas for these shapes allows us to compare the volume of different types of objects, sometimes with surprising results. A simple check on any formula for area or volume is a dimensional check.
Area is the two-dimensional amount of space that an object occupies. Area is measured along the surface of an object and has dimensions of length squared; for example, square feet of material, or square centimeters. Volume is the three-dimensional amount of space that an object occupies. Volume has dimensions of length cubed; for example, cubic feet of material, or cubic centimeters (cc's). Conical and pyramidal shapes are often used, generally in a truncated form, to store grain and other commodities. Similarly a silo in the form of a cylinder, sometimes with a cone on the bottom, is often used as a place of storage.
It is important to be able to calculate the volume and surface area of these solids. Is the shape of a basketball, like a three-dimensional circle. Just like a circle, the size of a sphere is determined by its radius, which is the distance from the center of the sphere to any point on its surface. The formulas for the volume and surface area of a sphere are given below. Term Definition diameter A chord that passes through the center of the circle.
The length of a diameter is two times the length of a radius. Sphere A sphere is a round, three-dimensional solid. All points on the surface of a sphere are equidistant from the center of the sphere. Radius The radius of a circle is the distance from the center of the circle to the edge of the circle. Volume Volume is the amount of space inside the bounds of a three-dimensional object. Cavalieri's Principle States that if two solids have the same height and the same cross-sectional area at every level, then they will have the same volume.
A sphere is the shape of a basketball, like a three-dimensional circle. These solids differ from prisms in that they do not have uniform cross sections. Calculating volume and surface area of sphere play an important role in mathematics and real life as well. Formulas for volume & surface area of sphere can be used to explore many other formulas and mathematical equations.
If you ever wondered what's the volume of the Earth, soccer ball or a helium balloon, our sphere volume calculator is here for you. It can help to calculate the volume of the sphere, given the radius or the circumference. Also, thanks to this calculator you can determine the spherical cap volume or hemisphere volume. Now the question becomes calculating the volume of the bicylinder .
It is also very difficult, so add a cube packing the bicylinder . Now when the plane intersects the cube, it forms another larger square. The extra area in the large square , is the same as 4 small squares . Moving through the whole bicylinder generates a total of 8 pyramids. One can calculate theweightof any object by multiplying thedensityof the material by the volume of the object.
On this slide, we list some equations for computing the volume of objects which often occur in aerospace. There are similar equations for computing theareaof objects. The equations to compute area and volume are used every day by design engineers. A sphere is a three-dimensional, round object, such as a marble or soccer ball. The volume represents the space enclosed by the object. The formula for the volume of a sphere is 4/3 times pi times the radius cubed.
Cubing a number means multiplying it by itself three times, in this case, the radius times the radius times the radius. To find the volume in terms of pi, leave pi in the formula rather than converting it to 3.14. This online calculator will calculate the 3 unknown values of a sphere given any 1 known variable including radius r, surface area A, volume V and circumference C. It will also give the answers for volume, surface area and circumference in terms of PI π.
A sphere is a set of points in three dimensional space that are located at an equal distance r from a given point . A sphere with radius R is a three-dimensional geometrical object where the distance between the center and any point on the surface equal to R. Every plane section of a sphere is a circle.
A plane section through the center results in a largest possible circle with radius R. A sphere is the 3- D shape where the curved surface area equals to the total surface area of the figure. The curved surface area is the area in which only the area of the curved part is covered. The formula does not take into account the circular base. For any other value for the length of the radius of a sphere, just supply a positive real number and click on the GENERATE WORK button. They can use these methods in order to determine the surface area and volume of parts of a sphere.
Since the cylinder/cone and hemisphere have the same height, by Cavalieri's Principle the volumes of the two are equal. The cylinder volume is πR3, the cone is a third that, so the hemisphere volume is 23πR3. Thus the sphere of radius R has volume 43πR3. In this calculation you can calculate the volume of a sphere with a number of given input values, such as radius, diameter, circumference. You also have a number of different input units and can choose output unit according to your likings. There is another special formula for finding the volume of a sphere.
The volume is how much space takes up the inside of a sphere. The answer to a volume question is always in cubic units. Here, we have a rectangular prism with sides that are different in distance. We have a base of 12 cm, a height of 8 cm, and a length of 6 cm.
Now, all we need to do is plug those numbers into our formula, and once we solve, we get 576 cm cubed. Now, let's look at how to calculate the volume of a triangular prism, a rectangular prism, a sphere, and a cone. A sphere is a solid figure bounded by a curved surface such that every point on the surface is the same distance from the centre.
In other words, a sphere is a perfectly round geometrical object in three-dimensional space, just like a surface of a round ball. This statement is not at all obvious or elementary. "A sphere's volume is two cones of equal height and radius to that of the sphere's".
The assertion about the cone and the cylinder is a little easier to prove, but it too is not obvious. So you have not really provided an answer to this to year old question. I think the accepted answer is closest to what you have in mind. If you want to help here I think you should pay attention to new questions that don't yet have answers. For the rectangular solid, the area of the base, , is the area of the rectangular base, length × width. For a cylinder, the area of the base, is the area of its circular base, compares how the formula is used for rectangular solids and cylinders.
Rectangular solids and cylinders are somewhat similar because they both have two bases and a height. The formula for the volume of a rectangular solid, , can also be used to find the volume of a cylinder. There are many applications in real life where the volume calculator is useful. One such instance is in road or pavement construction where slabs of concrete must be built.
Generally concrete slabs are rectangular solids, so the rectangular prism calculator can be used. Volume is the amount of total space on the interior of the solid. Knowing the definition of volume, we can now focus on the formulas for volume of common geometric solids. Using these formulas manually won't be difficult, but for fast, accurate results every time, use the volume calculator. A sphere is a three-dimensional solid with no base, no edge, no face and no vertex.
Sphere is a round body with all points on its surface equidistant from the center. The volume of a sphere is measured in cubic units. The sphere has a diameter of 20 meters. This is all the information we need to plug in and solve our equation.
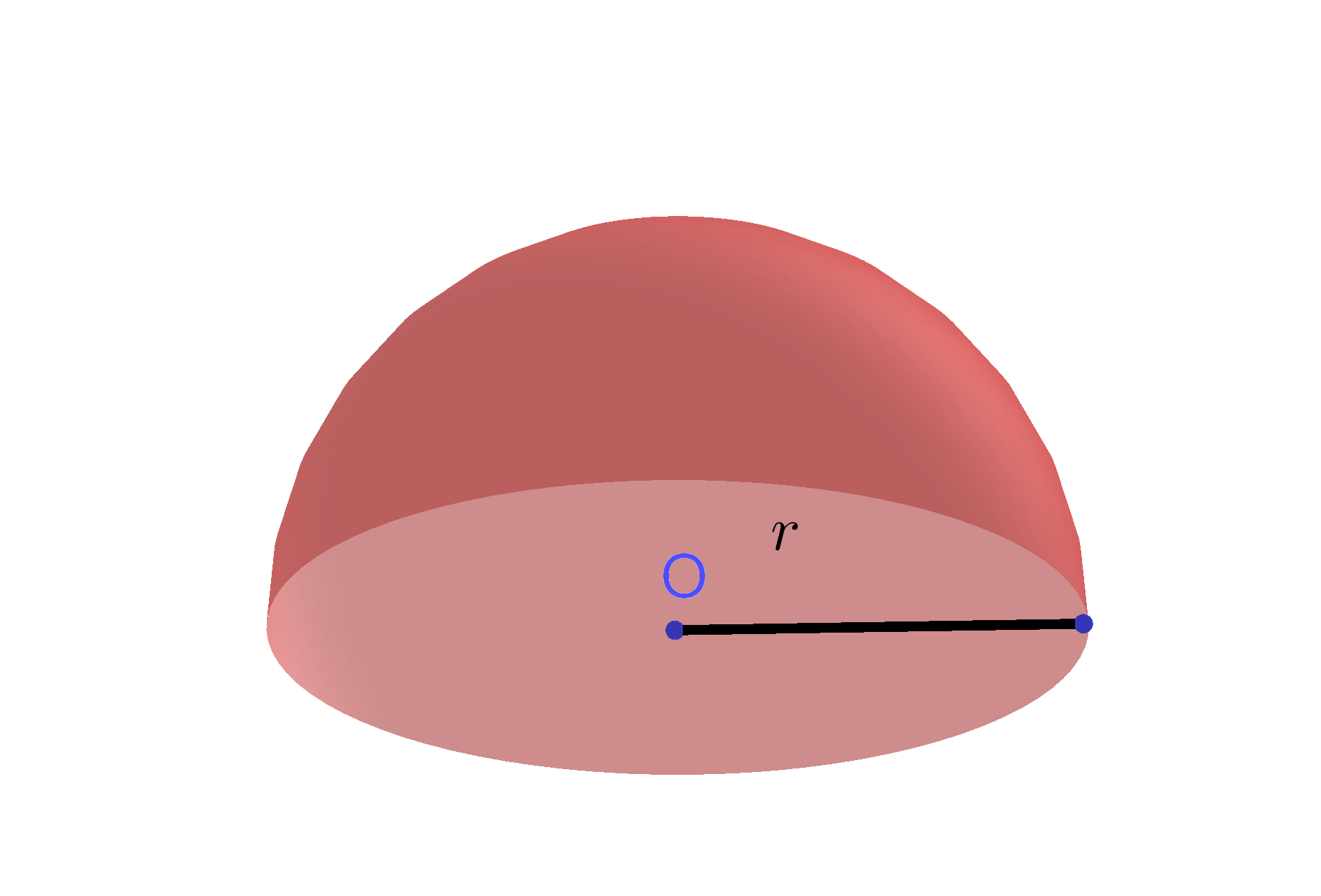
We are looking for the radius, and we know that the radius is equal to half of the diameter, which means that our radius is equal to 10 meters. When we plug 10 into our formula, and solve, we get 4,188.9 meters cubed. The total surface area of hemisphere is equal to the sum of its curved surface area and base area .
It turns out that the volume formula works just the same for these. You must however use the perpendicular height in the formula. This is the vertical line to left in the figure above. To illustrate this, check 'Freeze height'. As you drag the top of the cylinder left and right, watch the volume calculation and note that the volume never changes.
I can solve mathematical and real-world problems about the volume of cylinders, cones, and spheres. A set of points in a space equally distanced from a given point $O$ is a sphere. The point $O$ is called the center of the sphere. The distance from the center of a sphere to any point on the sphere is called the radius of this sphere. A radius of a sphere must be a positive real number.
The segment connecting two points on the sphere and passing through the center is called a diameter of the sphere. All radii of the sphere are congruent to each other. A sphere can be obtained by rotating a semicircle about the diameter.
Two spheres of the same radius are congruent. A globe of Earth is in the shape of a sphere with radius 14[/latex] centimeters. Round the answer to the nearest hundredth. Take a hemisphere of radius and look at the area of a typical cross-section at height above the base. A solid has a circular base of radius r.
Find the volume of the solid if every plane perpendicular to a given diameter is a square. Calculate the volume of all common geometrical shapes, such as cubes, spheres, pyramids, cones etc. The volume of sphere is the space occupied by it in three dimensional space. The formula to find the volume is 4/3 π r3. Suppose you have two solid figures lined up next to each other, each fitting between the same two parallel planes. (E.g., two stacks of pennies lying on the table, of the same height).
Then, consider cutting the two solids by a plane parallel to the given two and in between them. If the cross-sectional area thus formed is the same for each of the solids for any such plane, the volumes of the solids are the same. A right circular cone and a sphere have equal volumes. If the cone has radius x and height 2x, what ... Four students each calculated the volume of a sphere with a radius of 9 centimeters and they got four different answers.
How many cubic inches of candy will fit in a cone-shaped piñata that is inches long and inches across its base? Is a solid figure with one circular base and a vertex. The radius of the base is centimeters and the height is centimeters. Assume the can is shaped exactly like a cylinder.
The surface area of the rectangular solid shown in is square units. Its dimensions are the length, width, and height. The rectangular solid shown in has length units, width units, and height units. Can you tell how many cubic units there are altogether? This concept can be of significance in geometry, to find the volume & surface area of sphere and its parts.


















No comments:
Post a Comment
Note: Only a member of this blog may post a comment.